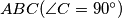
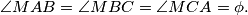
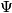
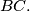
Let be the point inside the right-angled triangle such that Let be the acute angle between the medians of and Prove that
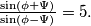
%V0
$(BUL 4)$ Let $M$ be the point inside the right-angled triangle $ABC (\angle C = 90^{\circ})$ such that $\angle MAB = \angle MBC = \angle MCA =\phi.$ Let $\Psi$ be the acute angle between the medians of $AC$ and $BC.$ Prove that $\frac{\sin(\phi+\Psi)}{\sin(\phi-\Psi)}= 5.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
be the point inside the right-angled triangle 
such that 
Let 
be the acute angle between the medians of 
and 
Prove that 