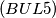
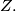
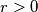
Let be a set of points in the plane. Suppose that there exists a pair of points that cannot be joined by a polygonal line not passing through any point of Let us call such a pair of points unjoinable. Prove that for each real there exists an unjoinable pair of points separated by distance
%V0
$(BUL 5)$ Let $Z$ be a set of points in the plane. Suppose that there exists a pair of points that cannot be joined by a polygonal line not passing through any point of $Z.$ Let us call such a pair of points unjoinable. Prove that for each real $r > 0$ there exists an unjoinable pair of points separated by distance $r.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
be a set of points in the plane. Suppose that there exists a pair of points that cannot be joined by a polygonal line not passing through any point of 
Let us call such a pair of points unjoinable. Prove that for each real 
there exists an unjoinable pair of points separated by distance 