IMO Shortlist 1969 problem 15
Dodao/la:
arhiva2. travnja 2012. 
Let
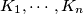
be nonnegative integers. Prove that
![K_1!K_2!\cdots K_n! \ge \left[\frac{K}{n}\right]!^n](/media/m/5/7/f/57fc388117dce24e551c1afc1962f1a9.png)
, where
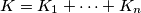
%V0
$(CZS 4)$ Let $K_1,\cdots , K_n$ be nonnegative integers. Prove that $K_1!K_2!\cdots K_n! \ge \left[\frac{K}{n}\right]!^n$, where $K = K_1 + \cdots + K_n$
Izvor: Međunarodna matematička olimpijada, shortlist 1969