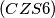
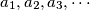
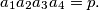
Let and be two real numbers. Find the first term of an arithmetic progression with difference such that Find the number of solutions in terms of and
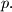
%V0
$(CZS 6)$ Let $d$ and $p$ be two real numbers. Find the first term of an arithmetic progression $a_1, a_2, a_3, \cdots$ with difference $d$ such that $a_1a_2a_3a_4 = p.$ Find the number of solutions in terms of $d$ and $p.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
and 
be two real numbers. Find the first term of an arithmetic progression 
with difference 
Find the number of solutions in terms of 