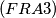
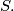
A polygon (not necessarily convex) with vertices in the lattice points of a rectangular grid is given. The area of the polygon is If is the number of lattice points that are strictly in the interior of the polygon and B the number of lattice points on the border of the polygon, find the number
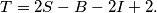
%V0
$(FRA 3)$ A polygon (not necessarily convex) with vertices in the lattice points of a rectangular grid is given. The area of the polygon is $S.$ If $I$ is the number of lattice points that are strictly in the interior of the polygon and B the number of lattice points on the border of the polygon, find the number $T = 2S- B -2I + 2.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
A polygon (not necessarily convex) with vertices in the lattice points of a rectangular grid is given. The area of the polygon is 
If 
is the number of lattice points that are strictly in the interior of the polygon and B the number of lattice points on the border of the polygon, find the number 