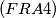
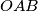
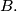
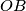
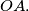
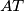
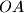
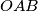
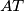
A right-angled triangle has its right angle at the point An arbitrary circle with center on the line is tangent to the line Let be the tangent to the circle different from ( is the point of tangency). Prove that the median from of the triangle intersects at a point such that
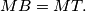
%V0
$(FRA 4)$ A right-angled triangle $OAB$ has its right angle at the point $B.$ An arbitrary circle with center on the line $OB$ is tangent to the line $OA.$ Let $AT$ be the tangent to the circle different from $OA$ ($T$ is the point of tangency). Prove that the median from $B$ of the triangle $OAB$ intersects $AT$ at a point $M$ such that $MB = MT.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
A right-angled triangle 
has its right angle at the point 
An arbitrary circle with center on the line 
is tangent to the line 
Let 
be the tangent to the circle different from 
(
is the point of tangency). Prove that the median from 
of the triangle 
such that 