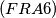
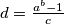
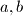
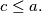
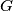
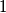
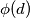
Consider the integer , where , and are positive integers and Prove that the set of integers that are between and and relatively prime to (the number of such integers is denoted by ) can be partitioned into subsets, each of which consists of elements. What can be said about the rational number
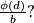
%V0
$(FRA 6)$ Consider the integer $d = \frac{a^b-1}{c}$, where $a, b$, and $c$ are positive integers and $c \le a.$ Prove that the set $G$ of integers that are between $1$ and $d$ and relatively prime to $d$ (the number of such integers is denoted by $\phi(d)$) can be partitioned into $n$ subsets, each of which consists of $b$ elements. What can be said about the rational number $\frac{\phi(d)}{b}?$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Consider the integer 
, where 
, and 
are positive integers and 
Prove that the set 
of integers that are between 
and 
and relatively prime to 
) can be partitioned into 
subsets, each of which consists of 
elements. What can be said about the rational number 