IMO Shortlist 1969 problem 24
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0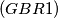 The polynomial
The polynomial 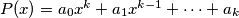 , where
, where 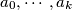 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if  is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if  is divisible by
is divisible by  , then
, then 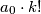 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 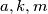 are positive integers such that
are positive integers such that 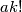 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial  with leading term
with leading term 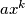 can be found that is divisible by
can be found that is divisible by 
Izvor: Međunarodna matematička olimpijada, shortlist 1969
 Školjka
Školjka 
