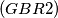
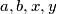
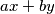
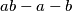
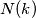
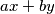
Let be positive integers such that and have no common divisor greater than . Prove that the largest number not expressible in the form is . If is the largest number not expressible in the form in only ways, find
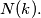
%V0
$(GBR 2)$ Let $a, b, x, y$ be positive integers such that $a$ and $b$ have no common divisor greater than $1$. Prove that the largest number not expressible in the form $ax + by$ is $ab - a - b$. If $N(k)$ is the largest number not expressible in the form $ax + by$ in only $k$ ways, find $N(k).$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
be positive integers such that 
and 
have no common divisor greater than 
. Prove that the largest number not expressible in the form 
is 
. If 
is the largest number not expressible in the form 
ways, find 