IMO Shortlist 1969 problem 26
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0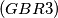 A smooth solid consists of a right circular cylinder of height
A smooth solid consists of a right circular cylinder of height  and base-radius
and base-radius  , surmounted by a hemisphere of radius
, surmounted by a hemisphere of radius  and center
and center 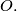 The solid stands on a horizontal table. One end of a string is attached to a point on the base. The string is stretched (initially being kept in the vertical plane) over the highest point of the solid and held down at the point
The solid stands on a horizontal table. One end of a string is attached to a point on the base. The string is stretched (initially being kept in the vertical plane) over the highest point of the solid and held down at the point  on the hemisphere such that
on the hemisphere such that 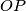 makes an angle
makes an angle 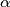 with the horizontal. Show that if
with the horizontal. Show that if 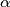 is small enough, the string will slacken if slightly displaced and no longer remain in a vertical plane. If then pulled tight through
is small enough, the string will slacken if slightly displaced and no longer remain in a vertical plane. If then pulled tight through  , show that it will cross the common circular section of the hemisphere and cylinder at a point
, show that it will cross the common circular section of the hemisphere and cylinder at a point  such that
such that 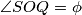 ,
,  being where it initially crossed this section, and
being where it initially crossed this section, and 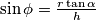 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1969
 Školjka
Školjka 
