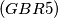
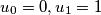
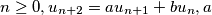
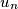
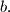
Let us define and for and being positive integers. Express as a polynomial in and Prove the result. Given that is prime, prove that divides
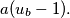
%V0
$(GBR 5)$ Let us define $u_0 = 0, u_1 = 1$ and for $n\ge 0, u_{n+2} = au_{n+1}+bu_n, a$ and $b$ being positive integers. Express $u_n$ as a polynomial in $a$ and $b.$ Prove the result. Given that $b$ is prime, prove that $b$ divides $a(u_b -1).$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let us define 
and for 
and 
being positive integers. Express 
as a polynomial in 
and 
Prove the result. Given that 