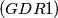
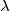
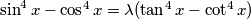
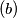
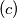
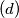
Find all real numbers such that the equation has no solution, has exactly one solution, has exactly two solutions, has more than two solutions (in the interval
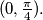
%V0
$(GDR 1)$ Find all real numbers $\lambda$ such that the equation $\sin^4 x - \cos^4 x = \lambda(\tan^4 x - \cot^4 x)$
$(a)$ has no solution,
$(b)$ has exactly one solution,
$(c)$ has exactly two solutions,
$(d)$ has more than two solutions (in the interval $(0, \frac{\pi}{4}).$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Find all real numbers 
such that the equation 
has no solution,
has exactly one solution,
has exactly two solutions,
has more than two solutions (in the interval 