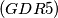
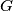
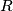
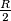
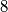
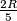
Given a ring in the plane bounded by two concentric circles with radii and , prove that we can cover this region with disks of radius . (A region is covered if each of its points is inside or on the border of some disk.)
%V0
$(GDR 5)$ Given a ring $G$ in the plane bounded by two concentric circles with radii $R$ and $\frac{R}{2}$, prove that we can cover this region with $8$ disks of radius $\frac{2R}{5}$. (A region is covered if each of its points is inside or on the border of some disk.)
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Given a ring 
in the plane bounded by two concentric circles with radii 
and 
, prove that we can cover this region with 
disks of radius 
. (A region is covered if each of its points is inside or on the border of some disk.)