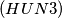
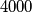
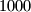
In the plane points are given such that each line passes through at most of these points. Prove that there exist disjoint quadrilaterals in the plane with vertices at these points.
%V0
$(HUN 3)$ In the plane $4000$ points are given such that each line passes through at most $2$ of these points. Prove that there exist $1000$ disjoint quadrilaterals in the plane with vertices at these points.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
In the plane 
points are given such that each line passes through at most 
of these points. Prove that there exist 
disjoint quadrilaterals in the plane with vertices at these points.