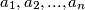
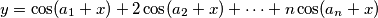
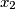
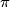
IMO2 If are real constants, and if has two zeros and whose difference is not a multiple of , prove that
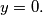
%V0
$(HUN 4)$IMO2 If $a_1, a_2, . . . , a_n$ are real constants, and if $y = \cos(a_1 + x) +2\cos(a_2+x)+ \cdots+ n \cos(a_n + x)$ has two zeros $x_1$ and $x_2$ whose difference is not a multiple of $\pi$, prove that $y = 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
IMO2 If 
are real constants, and if 
has two zeros 
and 
whose difference is not a multiple of 
, prove that 