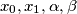
Given reals , find an expression for the solution of the system
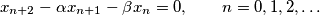
%V0
$(MON 2)$ Given reals $x_0, x_1, \alpha, \beta$, find an expression for the solution of the system $$x_{n+2} -\alpha x_{n+1} -\beta x_n = 0, \qquad n= 0, 1, 2, \ldots$$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Given reals 
, find an expression for the solution of the system 