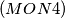
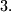
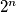
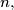
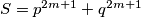
Let and be two prime numbers greater than Prove that if their difference is , then for any two integers and the number is divisible by
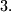
%V0
$(MON 4)$ Let $p$ and $q$ be two prime numbers greater than $3.$ Prove that if their difference is $2^n$, then for any two integers $m$ and $n,$ the number $S = p^{2m+1} + q^{2m+1}$ is divisible by $3.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
and 
be two prime numbers greater than 
Prove that if their difference is 
, then for any two integers 
and 
the number 
is divisible by