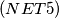
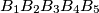
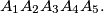
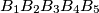
The bisectors of the exterior angles of a pentagon form another pentagon Construct from the given pentagon
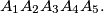
%V0
$(NET 5)$ The bisectors of the exterior angles of a pentagon $B_1B_2B_3B_4B_5$ form another pentagon $A_1A_2A_3A_4A_5.$ Construct $B_1B_2B_3B_4B_5$ from the given pentagon $A_1A_2A_3A_4A_5.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
The bisectors of the exterior angles of a pentagon 
form another pentagon 
Construct