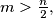
Let and be two natural numbers that have an equal number of digits in their decimal expansions. The first digits (from left to right) of the numbers and are equal. Prove that if then
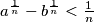
%V0
Let $a$ and $b$ be two natural numbers that have an equal number $n$ of digits in their decimal expansions. The first $m$ digits (from left to right) of the numbers $a$ and $b$ are equal. Prove that if $m >\frac{n}{2},$ then $a^{\frac{1}{n}} -b^{\frac{1}{n}} <\frac{1}{n}$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
and 
be two natural numbers that have an equal number 
of digits in their decimal expansions. The first 
digits (from left to right) of the numbers 
then 