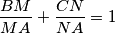
Given triangle with points and are in the sides and respectively. If , then prove that the centroid of lies on .
%V0
Given triangle $ABC$ with points $M$ and $N$ are in the sides $AB$ and $AC$ respectively.
If $\dfrac{BM}{MA} +\dfrac{CN}{NA} = 1$ , then prove that the centroid of $ABC$ lies on $MN$ .
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
with points 
and 
are in the sides 
and 
respectively. 
, then prove that the centroid of 
.