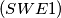
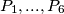
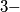
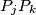
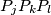
Six points are given in dimensional space such that no four of them lie in the same plane. Each of the line segments is colored black or white. Prove that there exists one triangle whose edges are of the same color.
%V0
$(SWE 1)$ Six points $P_1, . . . , P_6$ are given in $3-$dimensional space such that no four of them lie in the same plane. Each of the line segments $P_jP_k$ is colored black or white. Prove that there exists one triangle $P_jP_kP_l$ whose edges are of the same color.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Six points 
are given in 
dimensional space such that no four of them lie in the same plane. Each of the line segments 
is colored black or white. Prove that there exists one triangle 
whose edges are of the same color.