IMO Shortlist 1969 problem 61
Dodao/la:
arhiva2. travnja 2012. 
Let
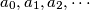
be determined with
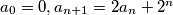
. Prove that if

is power of

, then so is

%V0
$(SWE 4)$ Let $a_0, a_1, a_2, \cdots$ be determined with $a_0 = 0, a_{n+1} = 2a_n + 2^n$. Prove that if $n$ is power of $2$, then so is $a_n$
Izvor: Međunarodna matematička olimpijada, shortlist 1969