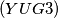
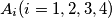
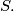
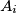
Let four points in the plane determine four triangles. In each of these triangles we choose the smallest angle. The sum of these angles is denoted by What is the exact placement of the points if ?
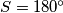
%V0
$(YUG 3)$ Let four points $A_i (i = 1, 2, 3, 4)$ in the plane determine four triangles. In each of these triangles we choose the smallest angle. The sum of these angles is denoted by $S.$ What is the exact placement of the points $A_i$ if $S = 180^{\circ}$?
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let four points 
in the plane determine four triangles. In each of these triangles we choose the smallest angle. The sum of these angles is denoted by 
What is the exact placement of the points 
if 
?