IMO Shortlist 1970 problem 1
Dodao/la:
arhiva2. travnja 2012. Consider a regular

-gon and the

diagonals of it that pass through its center. Let

be a point of the inscribed circle and let
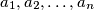
be the angles in which the diagonals mentioned are visible from the point

. Prove that
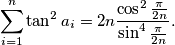
%V0
Consider a regular $2n$-gon and the $n$ diagonals of it that pass through its center. Let $P$ be a point of the inscribed circle and let $a_1, a_2, \ldots , a_n$ be the angles in which the diagonals mentioned are visible from the point $P$. Prove that
$$\sum_{i=1}^n \tan^2 a_i = 2n \frac{\cos^2 \frac{\pi}{2n}}{\sin^4 \frac{\pi}{2n}}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1970