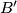
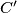
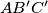
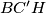
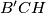
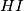
In the triangle let and be the midpoints of the sides and respectively and the foot of the altitude passing through the vertex . Prove that the circumcircles of the triangles ,, and have a common point and that the line passes through the midpoint of the segment
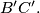
%V0
In the triangle $ABC$ let $B'$ and $C'$ be the midpoints of the sides $AC$ and $AB$ respectively and $H$ the foot of the altitude passing through the vertex $A$. Prove that the circumcircles of the triangles $AB'C'$,$BC'H$, and $B'CH$ have a common point $I$ and that the line $HI$ passes through the midpoint of the segment $B'C'.$
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
let 
and 
be the midpoints of the sides 
and 
respectively and 
the foot of the altitude passing through the vertex 
. Prove that the circumcircles of the triangles 
,
, and 
have a common point 
and that the line 
passes through the midpoint of the segment 