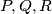
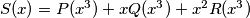
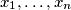
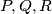
Let be polynomials and let be a polynomial of degree whose roots are distinct. Construct with the aid of the polynomials a polynomial of degree that has the roots
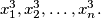
%V0
Let $P,Q,R$ be polynomials and let $S(x) = P(x^3) + xQ(x^3) + x^2R(x^3)$ be a polynomial of degree $n$ whose roots $x_1,\ldots, x_n$ are distinct. Construct with the aid of the polynomials $P,Q,R$ a polynomial $T$ of degree $n$ that has the roots $x_1^3 , x_2^3 , \ldots, x_n^3.$
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
be polynomials and let 
be a polynomial of degree 
whose roots 
are distinct. Construct with the aid of the polynomials 
of degree 