IMO Shortlist 1971 problem 1
Dodao/la:
arhiva2. travnja 2012. Consider a sequence of polynomials
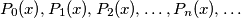
, where
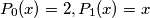
and for every
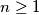
the following equality holds:
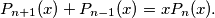
Prove that there exist three real numbers
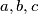
such that for all
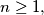
![(x^2 - 4)[P_n^2(x) - 4] = [aP_{n+1}(x) + bP_n(x) + cP_{n-1}(x)]^2.](/media/m/5/9/a/59a55695f2aa8a146a7400a5bdb3a335.png)
%V0
Consider a sequence of polynomials $P_0(x), P_1(x), P_2(x), \ldots, P_n(x), \ldots$, where $P_0(x) = 2, P_1(x) = x$ and for every $n \geq 1$ the following equality holds:
$$P_{n+1}(x) + P_{n-1}(x) = xP_n(x).$$
Prove that there exist three real numbers $a, b, c$ such that for all $n \geq 1,$
$$(x^2 - 4)[P_n^2(x) - 4] = [aP_{n+1}(x) + bP_n(x) + cP_{n-1}(x)]^2.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1971