IMO Shortlist 1971 problem 3
Dodao/la:
arhiva2. travnja 2012. Knowing that the system
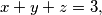
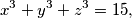
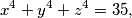
has a real solution
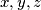
for which
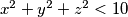
, find the value of
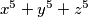
for that solution.
%V0
Knowing that the system
$$x + y + z = 3,$$ $$x^3 + y^3 + z^3 = 15,$$ $$x^4 + y^4 + z^4 = 35,$$
has a real solution $x, y, z$ for which $x^2 + y^2 + z^2 < 10$, find the value of $x^5 + y^5 + z^5$ for that solution.
Izvor: Međunarodna matematička olimpijada, shortlist 1971