IMO Shortlist 1971 problem 8
Dodao/la:
arhiva2. travnja 2012. Determine whether there exist distinct real numbers
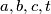
for which:
(i) the equation
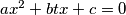
has two distinct real roots
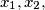
(ii) the equation
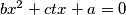
has two distinct real roots
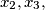
(iii) the equation
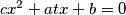
has two distinct real roots
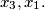
%V0
Determine whether there exist distinct real numbers $a, b, c, t$ for which:
(i) the equation $ax^2 + btx + c = 0$ has two distinct real roots $x_1, x_2,$
(ii) the equation $bx^2 + ctx + a = 0$ has two distinct real roots $x_2, x_3,$
(iii) the equation $cx^2 + atx + b = 0$ has two distinct real roots $x_3, x_1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1971