IMO Shortlist 1971 problem 9
Dodao/la:
arhiva2. travnja 2012. Let
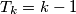
for
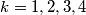
and
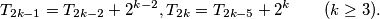
Show that for all

,
![1 + T_{2n-1} = \left[ \frac{12}{7}2^{n-1} \right] \quad \text{and} \quad 1 + T_{2n} = \left[ \frac{17}{7}2^{n-1} \right],](/media/m/6/a/9/6a9da69111a0b8b7fb9e7d7f4579e3fe.png)
where
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png)
denotes the greatest integer not exceeding

%V0
Let $T_k = k - 1$ for $k = 1, 2, 3,4$ and
$$T_{2k-1} = T_{2k-2} + 2^{k-2}, T_{2k} = T_{2k-5} + 2^k \qquad (k \geq 3).$$
Show that for all $k$,
$$1 + T_{2n-1} = \left[ \frac{12}{7}2^{n-1} \right] \quad \text{and} \quad 1 + T_{2n} = \left[ \frac{17}{7}2^{n-1} \right],$$
where $[x]$ denotes the greatest integer not exceeding $x.$
Izvor: Međunarodna matematička olimpijada, shortlist 1971