IMO Shortlist 1971 problem 11
Dodao/la:
arhiva2. travnja 2012. The matrix
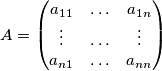
satisfies the inequality
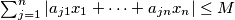
for each choice of numbers
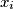
equal to
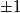
. Show that
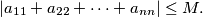
%V0
The matrix
$$A=\begin{pmatrix} a_{11} & \ldots & a_{1n} \\ \vdots & \ldots & \vdots \\ a_{n1} & \ldots & a_{nn} \end{pmatrix}$$
satisfies the inequality $\sum_{j=1}^n |a_{j1}x_1 + \cdots+ a_{jn}x_n| \leq M$ for each choice of numbers $x_i$ equal to $\pm 1$. Show that
$$|a_{11} + a_{22} + \cdots+ a_{nn}| \leq M.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1971