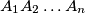
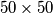
A broken line is drawn in a square, so that the distance from any point of the square to the broken line is less than . Prove that its total length is greater than
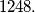
%V0
A broken line $A_1A_2 \ldots A_n$ is drawn in a $50 \times 50$ square, so that the distance from any point of the square to the broken line is less than $1$. Prove that its total length is greater than $1248.$
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
is drawn in a 
square, so that the distance from any point of the square to the broken line is less than 
. Prove that its total length is greater than 