IMO Shortlist 1972 problem 1
Dodao/la:
arhiva2. travnja 2012. 
and

are real-valued functions defined on the real line. For all

and
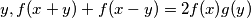
.

is not identically zero and
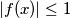
for all

. Prove that
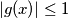
for all

.
%V0
$f$ and $g$ are real-valued functions defined on the real line. For all $x$ and $y, f(x+y)+f(x-y)=2f(x)g(y)$. $f$ is not identically zero and $|f(x)|\le1$ for all $x$. Prove that $|g(x)|\le1$ for all $x$.
Izvor: Međunarodna matematička olimpijada, shortlist 1972