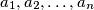
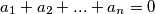
The least number is and the greatest number is among satisfying . Prove that
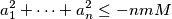
%V0
The least number is $m$ and the greatest number is $M$ among $a_1 ,a_2 ,\ldots,a_n$ satisfying $a_1 +a_2 +...+a_n =0$. Prove that
$$a_1^2 +\cdots +a_n^2 \le-nmM$$
Izvor: Međunarodna matematička olimpijada, shortlist 1972
Školjka 
and the greatest number is 
among 
satisfying 
. Prove that