IMO Shortlist 1973 problem 1
Dodao/la:
arhiva2. travnja 2012. Let a tetrahedron

be inscribed in a sphere

. Find the locus of points

inside the sphere

for which the equality
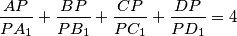
holds, where
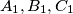
, and
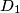
are the intersection points of

with the lines
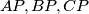
, and
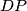
, respectively.
%V0
Let a tetrahedron $ABCD$ be inscribed in a sphere $S$. Find the locus of points $P$ inside the sphere $S$ for which the equality
$$\frac{AP}{PA_1}+\frac{BP}{PB_1}+\frac{CP}{PC_1}+\frac{DP}{PD_1}=4$$
holds, where $A_1,B_1, C_1$, and $D_1$ are the intersection points of $S$ with the lines $AP,BP,CP$, and $DP$, respectively.
Izvor: Međunarodna matematička olimpijada, shortlist 1973