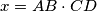
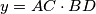
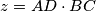
Given a tetrahedron , let , , and . Prove that there exists a triangle with edges
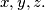
%V0
Given a tetrahedron $ABCD$, let $x = AB \cdot CD$, $y = AC \cdot BD$, and $z = AD \cdot BC$. Prove that there exists a triangle with edges $x, y, z.$
Izvor: Međunarodna matematička olimpijada, shortlist 1973
Školjka 
, let 
, 
, and 
. Prove that there exists a triangle with edges 