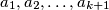
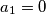
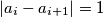
Prove that there are exactly arrays of nonnegative integers such that and for
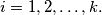
%V0
Prove that there are exactly $\binom{k}{[k/2]}$ arrays $a_1, a_2, \ldots , a_{k+1}$ of nonnegative integers such that $a_1 = 0$ and $|a_i-a_{i+1}| = 1$ for $i = 1, 2, \ldots , k.$
Izvor: Međunarodna matematička olimpijada, shortlist 1973
Školjka 
![\binom{k}{[k/2]}](/media/m/4/b/2/4b281ba757f46151539d6a54187bf655.png)
arrays 
of nonnegative integers such that 
and 
for 