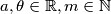
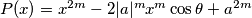
Given , and , factorize as a product of real quadratic polynomials.
%V0
Given $a, \theta \in \mathbb R, m \in \mathbb N$, and $P(x) = x^{2m}- 2|a|^mx^m \cos \theta +a^{2m}$, factorize $P(x)$ as a product of $m$ real quadratic polynomials.
Izvor: Međunarodna matematička olimpijada, shortlist 1973
Školjka 
, and 
, factorize 
as a product of 
real quadratic polynomials.