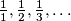
Prove that the squares with sides may be put into the square with side in such a way that no two of them have any interior point in common.
%V0
Prove that the squares with sides $\frac{1}{1}, \frac{1}{2}, \frac{1}{3},\ldots$ may be put into the square with side $\frac{3}{2}$ in such a way that no two of them have any interior point in common.
Izvor: Međunarodna matematička olimpijada, shortlist 1974
Školjka 
may be put into the square with side 
in such a way that no two of them have any interior point in common.