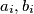
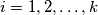
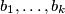
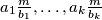
Let be coprime positive integers for , and the least common multiple of . Prove that the greatest common divisor of equals the greatest common divisor of
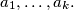
%V0
Let $a_i, b_i$ be coprime positive integers for $i = 1, 2, \ldots , k$, and $m$ the least common multiple of $b_1, \ldots , b_k$. Prove that the greatest common divisor of $a_1 \frac{m}{b_1} , \ldots, a_k \frac{m}{b_k}$ equals the greatest common divisor of $a_1, \ldots , a_k.$
Izvor: Međunarodna matematička olimpijada, shortlist 1974
Školjka 
be coprime positive integers for 
, and 
the least common multiple of 
. Prove that the greatest common divisor of 
equals the greatest common divisor of 