IMO Shortlist 1974 problem 9
Dodao/la:
arhiva2. travnja 2012. Let
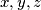
be real numbers each of whose absolute value is different from
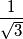
such that
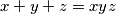
. Prove that
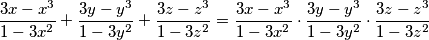
%V0
Let $x, y, z$ be real numbers each of whose absolute value is different from $\displaystyle \frac{1}{\sqrt 3}$ such that $x + y + z = xyz$. Prove that
$$\frac{3x-x^{3}}{1-3x^{2}}+\frac{3y-y^{3}}{1-3y^{2}}+\frac{3z-z^{3}}{1-3z^{2}}=\frac{3x-x^{3}}{1-3x^{2}}\cdot\frac{3y-y^{3}}{1-3y^{2}}\cdot\frac{3z-z^{3}}{1-3z^{2}}$$
Izvor: Međunarodna matematička olimpijada, shortlist 1974