IMO Shortlist 1975 problem 5
Dodao/la:
arhiva2. travnja 2012. Let

be the set of all positive integers that do not contain the digit

(base

). If
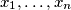
are arbitrary but distinct elements in

, prove that
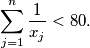
%V0
Let $M$ be the set of all positive integers that do not contain the digit $9$ (base $10$). If $x_1, \ldots , x_n$ are arbitrary but distinct elements in $M$, prove that
$$\sum_{j=1}^n \frac{1}{x_j} < 80 .$$
Izvor: Međunarodna matematička olimpijada, shortlist 1975