IMO Shortlist 1975 problem 7
Dodao/la:
arhiva2. travnja 2012. Prove that from
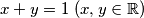
it follows that
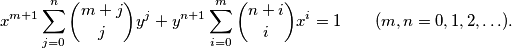
%V0
Prove that from $x + y = 1 \ (x, y \in \mathbb R)$ it follows that
$$x^{m+1} \sum_{j=0}^n \binom{m+j}{j} y^j + y^{n+1} \sum_{i=0}^m \binom{n+i}{i} x^i = 1 \qquad (m, n = 0, 1, 2, \ldots ).$$
Izvor: Međunarodna matematička olimpijada, shortlist 1975