IMO Shortlist 1975 problem 12
Dodao/la:
arhiva2. travnja 2012. Consider on the first quadrant of the trigonometric circle the arcs
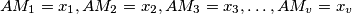
, such that
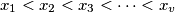
. Prove that
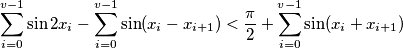
%V0
Consider on the first quadrant of the trigonometric circle the arcs $AM_1 = x_1,AM_2 = x_2,AM_3 = x_3, \ldots , AM_v = x_v$ , such that $x_1 < x_2 < x_3 < \cdots < x_v$. Prove that
$$\sum_{i=0}^{v-1} \sin 2x_i - \sum_{i=0}^{v-1} \sin (x_i- x_{i+1}) < \frac{\pi}{2} + \sum_{i=0}^{v-1} \sin (x_i + x_{i+1})$$
Izvor: Međunarodna matematička olimpijada, shortlist 1975