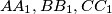
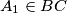
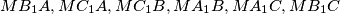
Let be a triangle with bisectors (, etc.) and their common point. Consider the triangles , and their inscribed circles. Prove that if four of these six inscribed circles have equal radii, then
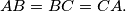
%V0
Let $ABC$ be a triangle with bisectors $AA_1,BB_1, CC_1$ ($A_1 \in BC$, etc.) and $M$ their common point. Consider the triangles $MB_1A, MC_1A,MC_1B,MA_1B,MA_1C,MB_1C$, and their inscribed circles. Prove that if four of these six inscribed circles have equal radii, then $AB = BC = CA.$
Izvor: Međunarodna matematička olimpijada, shortlist 1976
Školjka 
be a triangle with bisectors 
(
, etc.) and 
their common point. Consider the triangles 
, and their inscribed circles. Prove that if four of these six inscribed circles have equal radii, then 