IMO Shortlist 1976 problem 2
Dodao/la:
arhiva2. travnja 2012. Let
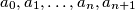
be a sequence of real numbers satisfying the following conditions:
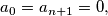
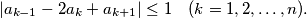
Prove that
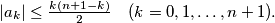
%V0
Let $a_0, a_1, \ldots, a_n, a_{n+1}$ be a sequence of real numbers satisfying the following conditions:
$$a_0 = a_{n+1 }= 0,$$ $$|a_{k-1} - 2a_k + a_{k+1}| \leq 1 \quad (k = 1, 2,\ldots , n).$$
Prove that $|a_k| \leq \frac{k(n+1-k)}{2} \quad (k = 0, 1,\ldots ,n + 1).$
Izvor: Međunarodna matematička olimpijada, shortlist 1976