IMO Shortlist 1976 problem 7
Dodao/la:
arhiva2. travnja 2012. Let
![I = (0, 1]](/media/m/b/3/1/b31662c00b12d2c1bafe576a0d350e1d.png)
be the unit interval of the real line. For a given number
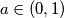
we define a map
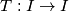
by the formula
if
{{ INVALID LATEX }}
Show that for every interval
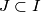
there exists an integer
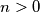
such that
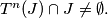
%V0
Let $I = (0, 1]$ be the unit interval of the real line. For a given number $a \in (0, 1)$ we define a map $T : I \to I$ by the formula
if
$$T (x, y) =\left\{\begin{array}{cc}x+(1-a),&\mbox{ if }0< x\leq a,\\ \text{ }\\ x-a, &\mbox{ if }a < x\leq 1.\end{array}\right$$
Show that for every interval $J \subset I$ there exists an integer $n > 0$ such that $T^n(J) \cap J \neq \emptyset.$
Izvor: Međunarodna matematička olimpijada, shortlist 1976