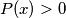
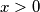
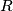
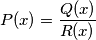
Let be a polynomial with real coefficients such that if . Prove that there exist polynomials and with nonnegative coefficients such that if
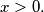
%V0
Let $P$ be a polynomial with real coefficients such that $P(x) > 0$ if $x > 0$. Prove that there exist polynomials $Q$ and $R$ with nonnegative coefficients such that $\displaystyle P(x) = \frac{Q(x)}{R(x)}$ if $x > 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1976
Školjka 
be a polynomial with real coefficients such that 
if 
. Prove that there exist polynomials 
and 
with nonnegative coefficients such that 
if 