IMO Shortlist 1976 problem 12
Dodao/la:
arhiva2. travnja 2012. The polynomial
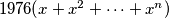
is decomposed into a sum of polynomials of the form
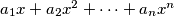
, where
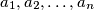
are distinct positive integers not greater than

. Find all values of

for which such a decomposition is possible.
%V0
The polynomial $1976(x+x^2+ \cdots +x^n)$ is decomposed into a sum of polynomials of the form $a_1x + a_2x^2 + \cdots + a_nx^n$, where $a_1, a_2, \ldots , a_n$ are distinct positive integers not greater than $n$. Find all values of $n$ for which such a decomposition is possible.
Izvor: Međunarodna matematička olimpijada, shortlist 1976