IMO Shortlist 1977 problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 A lattice point in the plane is a point both of whose coordinates are integers. Each lattice point has four neighboring points: upper, lower, left, and right. Let  be a circle with radius
be a circle with radius 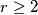 , that does not pass through any lattice point. An interior boundary point is a lattice point lying inside the circle
, that does not pass through any lattice point. An interior boundary point is a lattice point lying inside the circle  that has a neighboring point lying outside
that has a neighboring point lying outside  . Similarly, an exterior boundary point is a lattice point lying outside the circle
. Similarly, an exterior boundary point is a lattice point lying outside the circle  that has a neighboring point lying inside
that has a neighboring point lying inside  . Prove that there are four more exterior boundary points than interior boundary points.
. Prove that there are four more exterior boundary points than interior boundary points.
 be a circle with radius
be a circle with radius 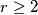 , that does not pass through any lattice point. An interior boundary point is a lattice point lying inside the circle
, that does not pass through any lattice point. An interior boundary point is a lattice point lying inside the circle  that has a neighboring point lying outside
that has a neighboring point lying outside  . Similarly, an exterior boundary point is a lattice point lying outside the circle
. Similarly, an exterior boundary point is a lattice point lying outside the circle  that has a neighboring point lying inside
that has a neighboring point lying inside  . Prove that there are four more exterior boundary points than interior boundary points.
. Prove that there are four more exterior boundary points than interior boundary points. Izvor: Međunarodna matematička olimpijada, shortlist 1977
 Školjka
Školjka 
